In order to play in some semblance of proper pitch, fretted instruments require compensation at the saddle in order to make allowance for the change in tension that occurs when a string is intoned. Unfortunately this correction at the saddle is only a partial solution to the problem. The compensation, which will allow the octave harmonic and the fretted harmonic for a particular string to sound as a well-tuned unison, is valid only for that particular position on the fingerboard. Presented here is a method that allows the simultaneous adjustment of the compensation for all of the other frets as well as maintaining the original octave compensation.
Before proceeding, a definition of several terms as used here and discussion of some of the limitations is in order. The Basic String Length (hereafter BSL) of the instrument is defined as the distance from the nut to the 12th fret multiplied by two. The Total String Length (TSL) is the BSL + Saddle Setback Dimension (SSD or setback). One further term is the Board Basis (BB), which regulates the positioning of the frets in the compensation system to be discussed. It is of vital importance to differentiate between the BSL of the instrument, which is an actual physical quantity, and the Board Basis of the fingerboard, which serves as a reference point for construction of the compensated board. They will have different, although close values. This system was developed for use with nylon string acoustic guitars, and the detailed discussion in this write-up will be confined to them. The general principle could be applied to other types of fretted instruments, but allowance must be made for the differing stretch properties of other string materials, as well as the differing action heights which will greatly influence the magnitude of the string stretch problems.
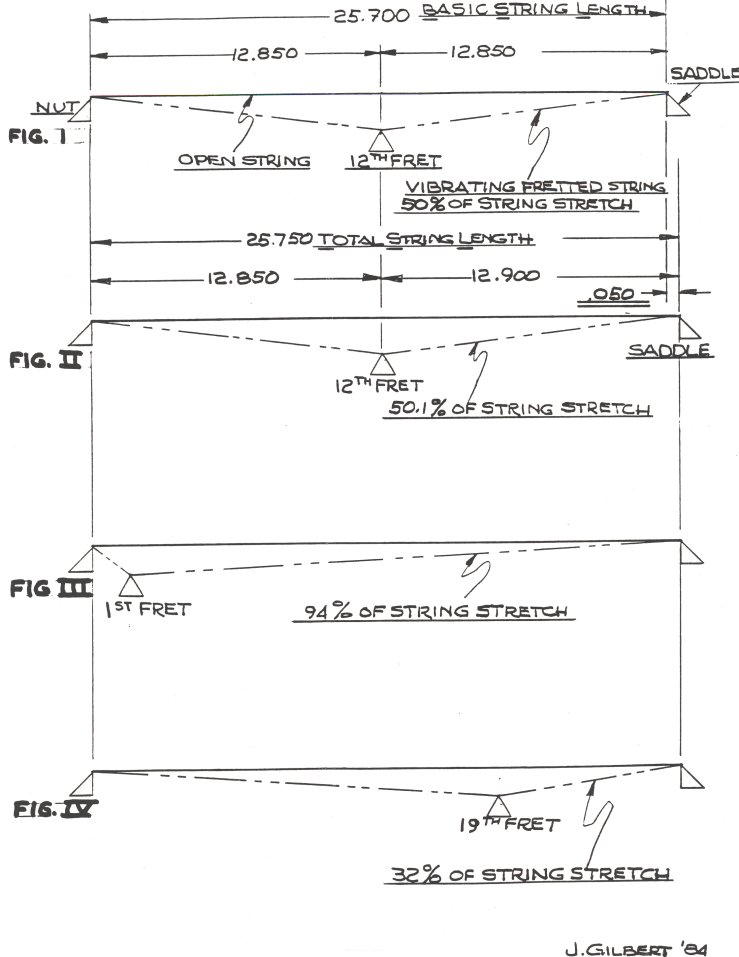
Referring to Figure I the original problem is depicted. The 12th fret is placed midway between the nut and the saddle to give a BSL and TSL of 25.700". The BSL and TSL are equal because there is no Saddle Setback Dimension (SSD). Of course this arrangement produces an instrument that plays sharp as the strings are intoned. The initial correction is shown in Figure II.
Here in this case the BSL has remained as 25.700" but the TSL has changed. It has increased by the new SSD of .050" to a figure of 25.750". This SSD is calculated to correct the sharping condition so that the intoned 12th fret, and the harmonic of the string at the twelfth fret (the true octave of the string) are identical in pitch. This works for the twelfth fret, but the instrument has more frets than that and this setback affects the other fret positions as well.
Figure III illustrates the conditions when a string is intoned at the first fret. The string must stretch and 94 %of that stretch takes place on the vibrating portion of the string. The SSD is insufficient to compensate for this stretch, and the string sounds sharp. In order to lower the intoned pitch to compensate for the stretch, the intoned portion of the string must be lengthened. The simplest solution since the saddle is fixed is to move the fret toward the nut by some amount so that the sharping condition is corrected.
Figure IV shows the situation at the other end of the fingerboard. Here again the string is stretched when it is intoned, but in this case 32% of the stretch takes place in the BSL for the guitar of 25.700. A critical point to understand when utilizing this system is the centrality of the BSL and its relationship to the BB. THE BOARD BASIS (BB) WILL HAVE NO PHYSICAL MANIFESTATION EXCEPT IN THE DISTANCE BETWEEN THE FRETS ON THE FINGERBOARD ONCE THE ADJUSTMENT OF THE NUT POSITION IS MADE TO MAKE THE NUT TO 12TH FRET DISTANCE THE SAME AS ONE HALF OF THE INSTRUMENT'S DESIGNED BSL! This notion is the apparent sticking point in prior attempts to describe this system. Below is a chart showing the actual nut to fret dimensions for the illustrated boards "A", "B" & "C". Included is a table "D" of the difference in position between a board fretted using a 25.700 BSL to determine all of the fret positions ("A") and one with the fret positions determined by the system ("C").
| Fret Number | "A" | "B" | "C" | "D" |
|---|---|---|---|---|
| 1 | 1.4424 | 1.4461 | 1.4133 | -0.0291 |
| 2 | 2.8039 | 2.8111 | 2.7783 | -0.0256 |
| 3 | 4.0890 | 4.0994 | 4.0666 | -0.0224 |
| 4 | 5.3019 | 5.3154 | 5.2826 | -0.0193 |
| 5 | 6.4468 | 6.4632 | 6.4304 | -0.0164 |
| 6 | 7.5274 | 7.5466 | 7.5138 | -0.0136 |
| 7 | 8.5473 | 8.5691 | 8.5363 | -0.0110 |
| 8 | 9.5100 | 9.5343 | 9.5015 | -0.0085 |
| 9 | 10.4187 | 10.4453 | 10.4125 | -0.0062 |
| 10 | 11 .2764 | 11.3052 | 11.2724 | -0.0040 |
| 11 | 12.0859 | 12.1168 | 12.0840 | -0.0019 |
| 12 | 12.8500 | 12.8828 | 12.8500 | 0.0000 |
| 13 | 13.5712 | 13.6059 | 13.5731 | +0.0019 |
| 14 | 14.2520 | 14.2883 | 14.2555 | +0.0035 |
| 15 | 14.8945 | 14.9325 | 14.8997 | +0.0052 |
| 16 | 15.5009 | 15.5405 | 15.5077 | +0.0068 |
| 17 | 16.0734 | 16.1144 | 16.0816 | +0.0082 |
| 18 | 16.6137 | 16.6561 | 16.6233 | +0.0096 |
| 19 | 17.1237 | 17.1674 | 17.1346 | +0.0109 |
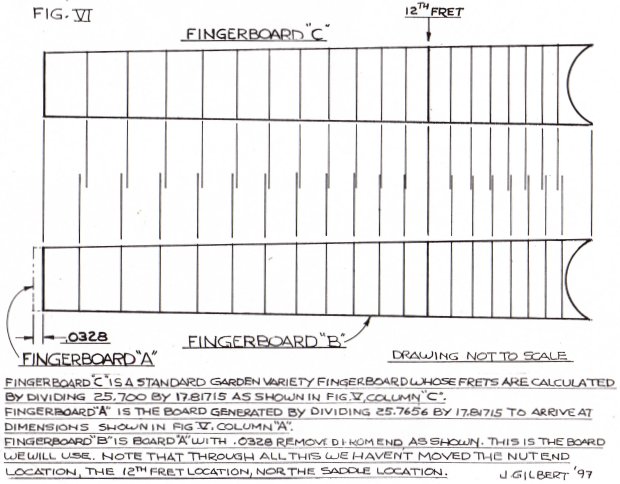
FINGERBOARD A BASED ON 25.700 BSL & BB FOR FRET POSITIONING
FINGERBOARD B BASED ON 25.7656 BSL & BB FOR FRET POSITIONING
FINGERBOARD C BASED ON 25.700 BSL & 25.7656 BB FOR FRET POSITIONING
"A" is the 25.700" BSL board "B" is the board cut to a 25.7656" BSL (BB ) "C" is Board "B" dimensions adjusted so as to cause the nut to 12th fret distance to be the same as board" A " "D" illustrates the difference between Boards" A" and "C". Negative numbers indicate the Board "C" nut to fret dimensions are smaller than board "A", Positive numbers indicate the board "C" nut to fret dimensions are larger than board "A".
The above chart demonstrates the ever-changing amount of compensation that is created by the use of this system. Column "D" shows the gradual shift in fret position from closer to the nut than theoretical at the nut end of the board to closer to the saddle than the theoretical dimension at the portion past the 12th fret.
The application of this method to new instruments of other string lengths depends on a few other factors. Action height is critical in selecting a BB, as it causes the amount of string stretch to change. A low action will require less compensation than a high one. (As an aside this also holds true for the SSD and action height) The height of the fret wire is also important, as high wire will tend to cause a sharping condition because of slightly increased string stretch, and low the opposite.
Assuming the instrument in question has a string length and action height that is relatively normal, and assuming nylon strings, the factor of 1.0025525 can be used to determine the BB. Proceed as follows. Determine the desired TSL. Subtract the SSD/ setback from this figure to arrive at the BSL for the instrument. Multiply the BSL for the instrument by the above factor to determine the BSL for the fingerboard, the BB. Using the procedure of BB/17.81715 determine the unadjusted nut to 1st fret distance. Compute all of these dimensions for the entire board. The procedure is identical to computing the fret positions from a given BSL. Instead of using the actual BSL of the instrument however, the BB is used, which functions as an artificial BSL for the purpose of generating the fret locations for the system. Also, rather than actually removing a portion of the fingerboard at the nut end, subtract from all of the above dimensions, (determined with the BB), an amount equal to half of the difference of the BB and BSL of the instrument. In effect a fingerboard will be generated for a longer string length, then the positions of the nut and 12th fret will be restored to those determined by the instrument's physical BSL.
An example: The TSL of a certain guitar is to be 650mm.
The designed SSD is 1.25mm. Therefore the BSL is 648.75mm (TSL-SSD). The BB will therefore be 1.0025525 x BSL of the instrument or 650.05mm. The Nut to fret dimensions calculated with this BB will be reduced by (650.05-648.75) divided by 2 or .65mm each. The table previously shown shows this for each nut to fret dimension. The difference between each dimension in the "B" and "C" columns is equal to 25.7656-25.700 divided by 2 or 0.0328". This is of course 1/2 the difference in value between the BB and the BSL.
To apply this method to an existing instrument requires a few conditions. First the original fret placement must be reasonably accurate. Second the saddle setback dimension must be proper (the intoned 12th fret and the harmonic there must be the same). Third there must be room at the saddle to shorten the string length slightly.
First determine the BSL of the existing instrument by measuring the dimension from the nut to the 12th fret and multiplying by 2. Check the SSD by measuring from the nut to the saddle (TSL) and subtracting the BSL from this dimension. If it is insufficient or excessive it is sometimes possible to correct it at the same time as the system is applied. Compute the new BSL by dividing the existing BSL by the 1.0025525 factor. Now is the tricky part. In order for the 12th fret to stay in its proper relative position, an equal amount must be removed from both the end of the fingerboard and from the string length at the saddle. This amount is again equal to one half of the difference between the desired BB (which is in this case the existing BSL) and the new BSL that has been computed by the above process.
In effect the total string length of the instrument is changed (shortened) in order to make the existing BB greater than the new BSL of the instrument by the 1.002... factor. Since the compensation was OK at the 12th fret it is necessary to shorten the string length at the saddle to preserve this compensation. If the instrument was somewhat under compensated at the twelfth fret (not enough SSD) then all is well, as it may be possible to leave the saddle alone and the dimension which would have been removed will serve instead to add to the SSD to bring it up to the required amount.
A final refinement to the system is the allowance of approximately 0.010-0.020 extra SSD for the 3rd string, as well as making sure that the bottom edge of the nut groove is not excessively broken.
To sum up. The system allows for correction of intonation errors caused by the variance in string tension when a string is intoned. It does this by first using the standard saddle correction that produces a proper unison between the intoned octave and the harmonic octave, and then modifying the positions of all the other frets to allow for the varying amount of string stretch encountered when intoning the string at other than the 12th fret. It is applicable to both a new construction board, and to existing instruments.